Month: February 2017

Neural coding 1: How to understand what a neuron is saying.

by

In this post I am diverting from my usual astrophotography theme and entering the world of computational neuroscience, a subject I studied for almost ten years. Computational neuroscience is a relatively new interdisciplinary branch of neuroscience that studies how areas of the brain and nervous system process and transmit information. An important and still unsolved question in computational neuroscience is how do neurons transmit information between themselves. This is known as the problem of neural coding and by solving this problem, we could potentially understand how all our cognitive functions are underpinned by neurons communicating with each other. So for the rest of this post I will attempt to discuss how we can read the neural code and why the code is so difficult to crack.

Since the twenties we have known that excited neurons communicate through electrical pulses called action potentials or spikes (see Figure 1). These spikes can quickly travel down the long axons of neurons to distant destinations before crossing a synapse and activating another neuron (form more information on neurons and synapses see here).

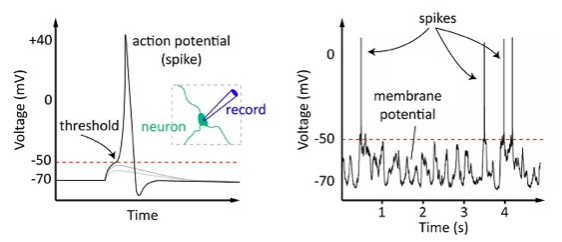
Figure 1. Neural action potentials. An action potential diagram is shown on the left as if recorded from inside a neuron (see inset). For an action potential arise and propagate through a neuron, it must reach a certain threshold (red dashed line). If it doesn’t the neuron will remain at rest. The right panel shows a real neurons firing spikes in the cortex of a mouse. Taken from Gentet LJ et al. (2010).

You would be forgiven for thinking that the neural coding problem is solved: neurons fire a spike when the see a stimulus they like and communicate this fact to other nearby neurons, while at other times they stay silent. Unfortunately, the situation is a bit more complex. Spikes are the basic symbol used by neurons to communicate, much like letters are the basic symbols of a written language. But letters only become meaningful when many are used together. This analogy is also true for neurons. When a neuron becomes excited it produces a sequence of spikes that, in theory, represent the stimuli the neuron is responding to. So if you can correctly interpret the meaning of spike sequences you could understand what a neuron is saying. In Figure 2, I show a hypothetical example of a neuron responding to a stimulus.

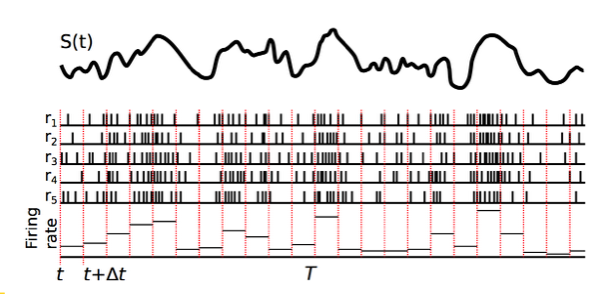
Figure 2. A stimulus (top trace) fluctuates over time (s(t)) and spikes from a hypothetical neuron are recorded. The stimulus is repeated 5 times producing 5 responses r1,2,3…5 shown below the stimulus. Each response is composed of spikes (vertical lines) and periods of silence. By counting the number of spikes within small time window lasting Δt seconds, we can calculate the firing rate of the neuron (bottom trace).

In this example a neuron is receiving an constantly fluctuating input. This is a bit like the signal you would expect to see from a neuron receiving a constant stream of inputs from thousands of other neurons. In response to this stimulus the receiving neuron constantly changes its spike firing rate. If we read this rate we can get a rough idea of what this neuron is excited by. In this case, the neuron fires faster when the stimulus is high and is almost silent when the stimulus is low. There is a mathematical method that can extract the stimulus that produces spikes, known as reverse correlation (Figure 3).

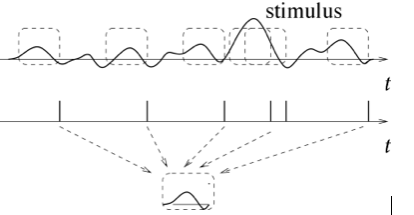
Figure 3. Reverse correlation can identify what feature of the stimulus (top) makes a neuron fire a spike (bottom). Stimulus samples are taken before each spike (vertical lines) and then averaged to produce a single stimulus trace representing the average stimulus that precedes a spike.

The method is actually very simple; each time a spike occurs we take a sample of the stimulus just before the spike. Hopefully many spikes are fired and we end up with many stimulus samples, in Figure 3 the samples are shown as dashed boxes over the stimulus. We then take these stimulus samples and average them together. If these spikes are being fired in response to a common feature in the stimulus we will be able to see this. This is therefore simple method of finding what a neuron actually responds to when it fires a spike. However, there are limitations to this procedure. For instance, if a neuron responds to multiple features within a stimulus then these will be averaged together leading to a misleading result. Also, this method assumes that the stimulus contains a wide selection of different stimulus fluctuations. If it doesn’t then you can never really know what a neuron is really responding to because you may not have stimulated it with anything it likes!

In my next two posts, I will discuss how more advanced methods from the realms of artificial intelligence and probability theory have helped neuroscientists more accurately extract the meaning of neural activity.

Post by: Daniel Elijah

Afforestation Vs reforestation

by

It is well known that deforestation is an increasing global problem. Even those with little scientific background are bombarded with information through social media, specifically regarding consequences of deforestation including global warming. Indeed, many charities, schools and individuals are now taking a stand and doing all they can to tackle this problem.

The planting of trees can be divided into two categories: afforestation and reforestation. Reforestation refers to planting trees on land that was previously forest whereas afforestation refers to planting trees on patches of land which were not previously covered in forest. The general idea behind both is: as many trees as possible, wherever possible.
However, ecology is a complex science. Are we focusing too much on carbon sequestration and not enough on the planets ecosystems as a whole? Are some ecosystems being neglected and forgotten? Perhaps. This article will cover some issues associated with afforestation and reforestation.

Reforestation is beneficial when trees have been previously removed. However, these new trees will never create exactly the same ecosystem as the original forest. Indeed, the original trees which were cleared may have been hundreds, even thousands of years old meaning that it may take many years for the new trees to catch up. In addition to this, rare species lost during the original deforestation may not be replaced, meaning extinction and a reduction of biodiversity could be inevitable.

Tropical grassy Biome

Afforestation can also have negative consequences especially if the tree planters don’t consider the environment they are introducing the new trees into. The idea of afforestation is to plant trees on patches of unused, degrading land. However, land which may appear degraded may actually house its own ecosystem, for example a Savanna or tropical grassy biome. Research has suggested that tropical grassy biomes are often misunderstood and neglected. These ecosystems can provide important ecological services. In addition to this, these ecosystems could contain rare species, which could be outcompeted by the introduction of new trees.Therefore, although carbon sequestration will increase, many ecosystems will be negatively affected or lost.

It has to be noted that both reforestation and afforestation can be advantageous when tackling global warming. However, possible negative impacts must also be taken into account in order to protect the planet as a whole. This can be achieved by ensuring that deforestation is kept to a minimum and afforestation only occurs on truly degraded land. There is desperate need for more research into areas of land before trees are planted upon them. The biggest challenge today is education. Charities, schools and individuals need to be made aware of this before it’s too late. Without awareness, irreversible damage can occur unknowingly. Effective conservation work requires more than just planning trees at random and this needs to be taken considered on a global scale.
If we don’t stand up for all of our precious ecosystems, who will?

Post by: Alice Brown

References:
http://www4.ncsu.edu/~wahoffma/publications/pdf/Parr2014TREE_TropicalGrassyBiomes_MisunderstoodNeglectedAndUnderThreat.pdf
https://pixabay.com/en/photos/plain/?cat=nature

 

Save

Save