The seemingly innocuous word ‘random’ is often misused in the English language. This is true of many words but I want to dedicate some time to discuss the word ‘random’ because of its fascinating mathematical meaning and the importance of truly random processes to the world around us.

What does random actually mean in mathematics?
Firstly lets talk about what it doesn’t mean. For most people, being random is akin to being strange, weird or erratic. This has become its common usage, the Oxford English Dictionary has a similar definition: ‘being made, done or happening without method or conscious decision’ (OED 10th Edition). So what’s the problem here? The issue is that the word random has a hidden mathematical meaning, something that most people are completely unaware of, even as the word emanates from their lips.
In mathematics, something that is random has no predictability or correlation. If you have a random sequence of numbers, then picking one number will give you no clue about what number came before it or what number will follow afterwards. It’s a very simple concept on paper but to actually calculate or observe truly random and unpredictable behaviour in the real world is very difficult. The problem is that in the natural world, almost every event that ever happens (for things larger than atoms) has an effect on something else which leads to a constantly growing web of interconnected events. Our reality is in fact a result of an almost infinite combination of interconnected events from the past affecting every aspect of the present. This interconnectivity means that most events that appear random such as the result of a dice throw or the positions of grains of sand on a beach are in fact predictable but only if you know all the smallest details of past events and how they affect each other.
Let’s take a simple coin throw as an example, on the surface the result (heads or tails) appears random and unpredictable).
However, a study by Persi Diaconis found that when a machine flips a coin with identical force and spin, the outcome is highly predicable. Not only that but different coins have different biases to fall on one particular side, and the result of a coin toss is highly dependent on the angle that the initial force is applied to the coin. All these factors are well known to magicians who can toss a coin is a seemingly natural way whilst being able to predict the outcome with amazing certainty.
Computers also suffer from the problem of non-randomness. When you command a computer to generate a sequence of random numbers it actually starts from a seed number (any number can be a seed) and then it runs a complex (but predicable) algorithm to generate seeming uncorrelated, random numbers. Here’s a gif of a program I made to illustrate random number generation…
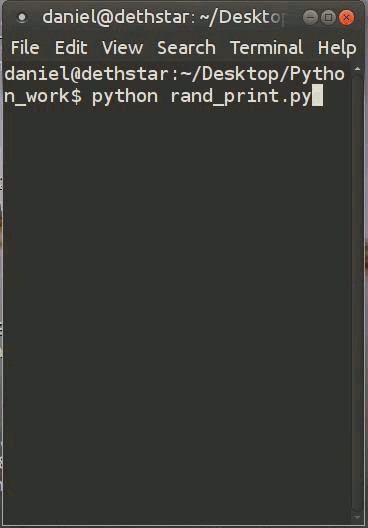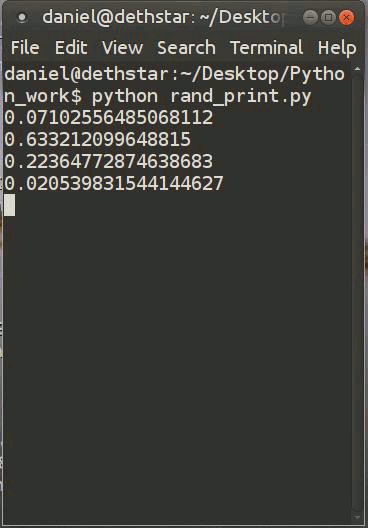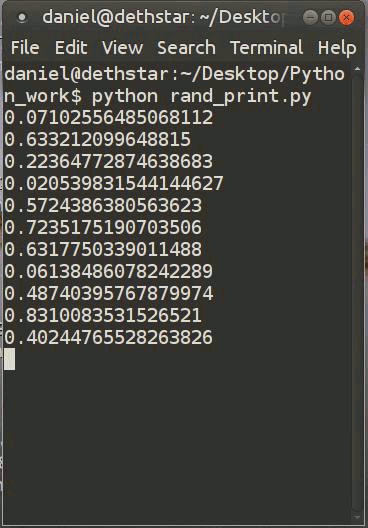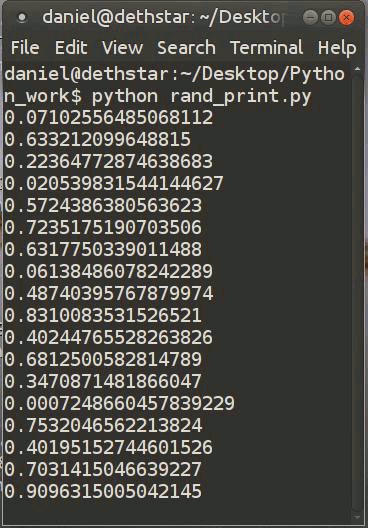
Because these numbers are generated from a fixed seed in a predictable way, we call these numbers psudo-random. They are not safe to use for encrypting data or securing your computer. To produce better randomness, some computers measure difficult-to-predict things such as the time of your keystrokes, or the electronic noise in a circuit.
My point is that most random events that we experience in everyday life are far from random. By labelling such things as random we are actually obscuring the fact that they only appear random because of our own lack of understanding about all the factors that control them.

So, are there any examples of truly random events? The answer is yes, but for these examples, you need to delve into the quantum world of atoms and electrons. In quantum mechanics, interactions and movements are not governed by basic cause and effect but by probability. For example, electrons do not orbit in circles around atoms, they appear and disappear within a cloud surrounding the atom. If you look close to an atomic nucleus (the dark area in the diagram – right) you may spot electrons appearing and disappearing but, you will never know exactly when or where this is going to happen (this event is random). The further you move from the nucleus the rarer these appearances and disappearances become, still following a random sequence.
When a radioactive element decays, the nuclei of its atoms change or shed mass. When you are observing trillions of atoms you can predict how many will decay per hour, but if you isolate just one atom you will never know exactly when it will decay.
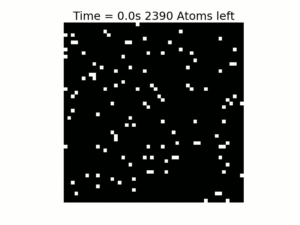
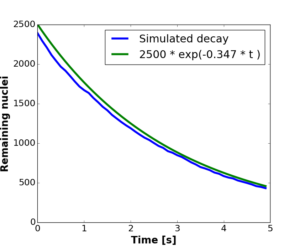
For me this final point is the most fascinating. When you look at a single randomly behaving system (like the decay of atoms or the movement of electrons) by themselves they appear completely unpredictable. If you look at a single black pixel (representing an undecayed atom) in the above left plot, there is no way to tell when it will decay and become white. However when you observe large numbers of them the random behaviour ‘smooths’ out to produce a predicable pattern; just look how the decay curve on the right is showing a clear, predictable decrease.
This idea of large-scale patterns emerging out of small scale randomness extends to our entire world. Everything we interact with and experience which can be though of as ultimately predictable is, in fact, composed of tiny particles moving about, interacting and decaying in a completely random and unpredictable way.
Pretty random really…
Post by: Daniel Elijah






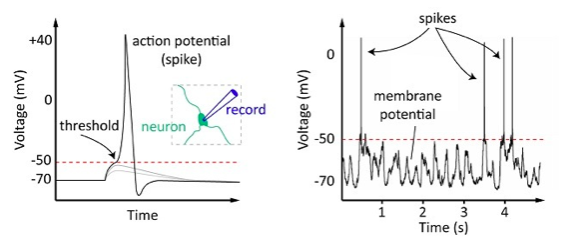




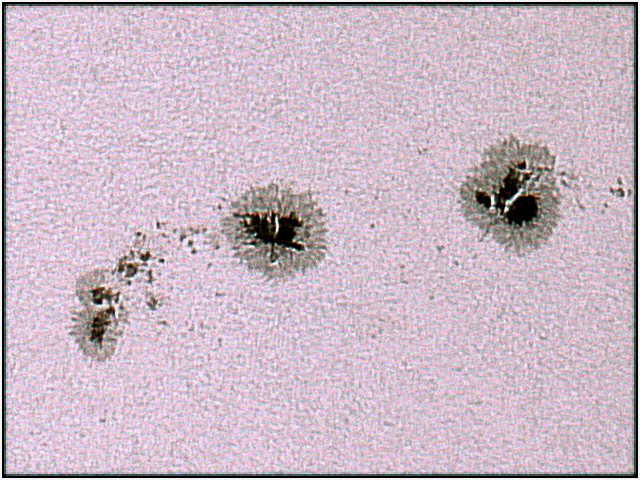



 This one is an error many newcomers to the hobby make, partly because of some pretty dodgy marketing – see the unobtainable views pictured on the very basic telescope above. Put simply, it is the expectation that a small telescope operated by someone with little experience will produce celestial views equaling the HST. If you search for a beginner telescope online and run through its reviews there will be a number complaining of blurry images, poor zoom and undefined galaxies. These limitations are sadly just unavoidable consequences of living under a turbulent atmosphere or owning a telescope that doesn’t have the HST’s 2.4m diameter aperture. In the end, I class this as one of the most damaging errors here because for those who make it astronomy becomes a frustration rather than a fascination. However, once you get familiar with the capabilities of your telescope/binoculars you quickly start to appreciate the significance of those faint smudges of light!
This one is an error many newcomers to the hobby make, partly because of some pretty dodgy marketing – see the unobtainable views pictured on the very basic telescope above. Put simply, it is the expectation that a small telescope operated by someone with little experience will produce celestial views equaling the HST. If you search for a beginner telescope online and run through its reviews there will be a number complaining of blurry images, poor zoom and undefined galaxies. These limitations are sadly just unavoidable consequences of living under a turbulent atmosphere or owning a telescope that doesn’t have the HST’s 2.4m diameter aperture. In the end, I class this as one of the most damaging errors here because for those who make it astronomy becomes a frustration rather than a fascination. However, once you get familiar with the capabilities of your telescope/binoculars you quickly start to appreciate the significance of those faint smudges of light!










